CONTEÚDOS E METODOLOGIAS DO ENSINO DE MATEMÁTICA

Quando uma curva é formada apenas por segmentos de reta, ela é chamada de linha poligonal, o que significa ter muitos lados ou ângulos. Ela pode ser aberta simples e não simples ou fechada simples.
I - As curvas fechadas simples são classificadas em convexas e não convexas.
II - Uma curva fechada é convexa quando todos os segmentos com extremidades A e B, estiverem contidos dentro da região interna.
III - Em qualquer polígono convexo, o número de lados, de ângulos e de vértices são iguais.
IV - Se existir algum vértice voltado para o interior do polígono, ele não será convexo.
V - As curvas fechadas simples dividem o plano em duas regiões: uma interna e a outro externa.
Assinale a alternativa que apresenta a sequência correta:
I, II e III
I, II, III e IV
II, III, IV e V
I, III e IV
I, II, III , IV e V
As propriedades da MULTIPLICAÇÃO são: propriedade de fechamento; comutativa, associativa, distributiva e elemento neutro.
Mas para que servem estas propriedades? Para facilitar o cálculo.
A compreensão de cada uma delas auxiliará resolver a operação mentalmente.
Para isso o professor NÃO deve apenas trabalhar a “decoreba” das propriedades, e sim, fazer o experimento que comprove cada uma delas. Isso porque muitas dessas propriedades são utilizadas no nosso cotidiano sem percebermos. Assim podemos afirmar que as propriedades das operações são artifícios criados para facilitar o cálculo.
Obs: A operação do item I, estará representando duas propriedades.
Com base neste estudo, analise as imagens abaixo e associe cada operação representada com a propriedade que foi aplicada. Em seguida assinale a sequencia correta.
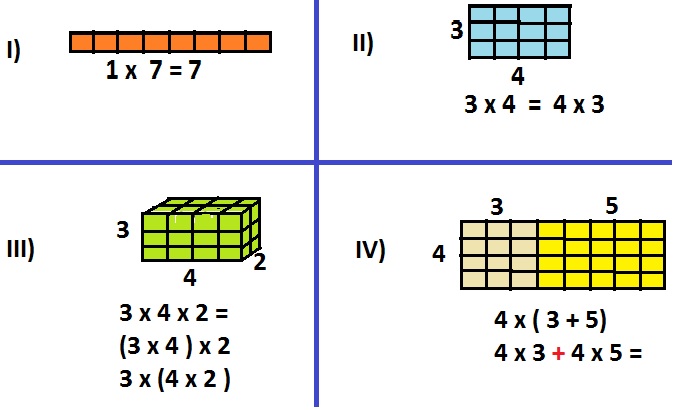
Fechamento e ou elemento neutro, distributiva, comutativa, associativa.
Fechamento e ou elemento neutro, comutativa, associativa, distributiva.
Associativa, fechamento e ou elemento neutro, distributiva, comutativa.
Fechamento e ou elemento neutro, comutativa, distributiva, associativa.
Fechamento e ou elemento neutro, associativa, comutativa, distributiva.
I - A partir do momento em que o homem abstraiu a ideia de número e a sua vida social foi se intensificando, houve a necessidade de contar conjuntos cada vez mais numerosos.
Porque:
II- Quando precisamos contar uma grande quantidade de coisas, separando os objetos em grupos, isso facilita a contagem, o que implica muitas situações. Os agrupamentos são necessários para facilitar o trabalho do homem.
A respeito dessas asserções, assinale a opção correta.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições falsas.
As frações são representações de partes do todo, e são escritas na forma n/d onde n e d são números naturais. E d é diferente de zero. Ao comparamos os valores de n (numerador) e d (denominador), poderemos definir o tipo da fração.
Sobre os tipos de fração existentes numere a segunda coluna de acordo com a primeira.
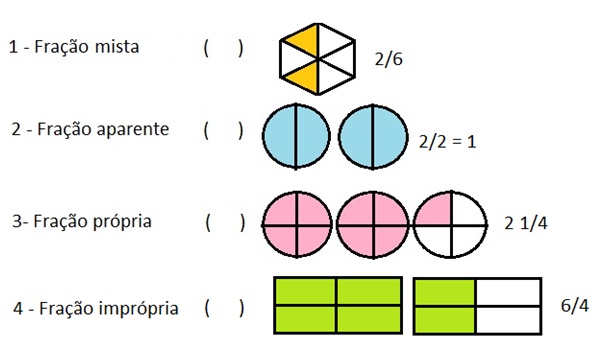
Está correto o que afirma em:
3, 2, 1, 4
1, 4, 3, 2
1, 2, 3, 4
3, 4, 2, 1
2, 3, 1, 4
Observe as frações abaixo,
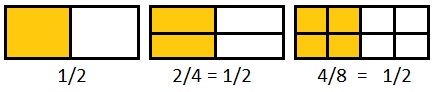
Veja que todas essas frações indicam a mesma parte da unidade considerada, ou seja, meia unidade. Dizemos que as frações 1/2, 2/4 e 4/8 são frações ___________________________, pois representam a mesma parte de um todo.
Qual das afirmativas abaixo completam corretamente a frase?
Está correto o que afirma em:
aparente
decimal
equivalente
impropria
irredutível
Leia as asserções abaixo.
I- Em uma multiplicação, o produto é sempre múltiplo de cada um dos fatores.
Porque
II- Para que um número seja múltiplo do outro, basta multiplicar esse número por um número natural.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições falsas.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A geometria é o ramo das matemáticas que se consagra ao estudo das propriedades e das medidas das figuras no espaço ou no plano. No seu desenvolvimento, a geometria usa noções tais como pontos, retas, planos e curvas, entre outras. (Disponível em: Conceito de geometria - O que é, Definição e Significado http://conceito.de/geometria#ixzz4YwcujrCW).

Euclides estudou os elementos primitivos (ponto, reta e plano) e formulou a Geometria Euclidiana. Com base nesse estudo numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
2, 3, 1, 1, 3
2, 1, 3, 1, 3
1, 3, 2, 1, 3
1, 2, 3, 1, 2
1, 2, 2, 3, 3
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Ponto, reta, reta, ponto e plano.
Ponto, plano, reta, plano e reta.
Ponto, plano, plano, ponto e reta.
Ponto, plano, reta, ponto e plano.
Plano, ponto, reta, ponto e reta.
Dois automóveis estão indo de A para B.
Observe o percurso que cada uma fez e responda a pergunta assinalando a alternativa correta.
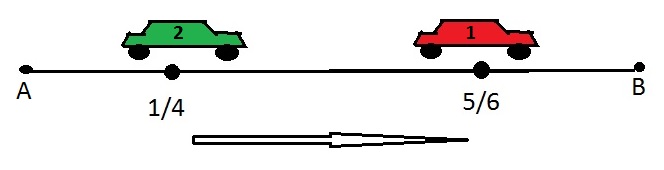
Qual a diferença entre o percurso do carro 1 e do carro 2?
I, II e III
I, II, III e IV
II, III, IV e V
I, III e IV
I, II, III , IV e V
As propriedades da MULTIPLICAÇÃO são: propriedade de fechamento; comutativa, associativa, distributiva e elemento neutro.
Mas para que servem estas propriedades? Para facilitar o cálculo.
A compreensão de cada uma delas auxiliará resolver a operação mentalmente.
Para isso o professor NÃO deve apenas trabalhar a “decoreba” das propriedades, e sim, fazer o experimento que comprove cada uma delas. Isso porque muitas dessas propriedades são utilizadas no nosso cotidiano sem percebermos. Assim podemos afirmar que as propriedades das operações são artifícios criados para facilitar o cálculo.
Obs: A operação do item I, estará representando duas propriedades.
Com base neste estudo, analise as imagens abaixo e associe cada operação representada com a propriedade que foi aplicada. Em seguida assinale a sequencia correta.

Fechamento e ou elemento neutro, distributiva, comutativa, associativa.
Fechamento e ou elemento neutro, comutativa, associativa, distributiva.
Associativa, fechamento e ou elemento neutro, distributiva, comutativa.
Fechamento e ou elemento neutro, comutativa, distributiva, associativa.
Fechamento e ou elemento neutro, associativa, comutativa, distributiva.
I - A partir do momento em que o homem abstraiu a ideia de número e a sua vida social foi se intensificando, houve a necessidade de contar conjuntos cada vez mais numerosos.
Porque:
II- Quando precisamos contar uma grande quantidade de coisas, separando os objetos em grupos, isso facilita a contagem, o que implica muitas situações. Os agrupamentos são necessários para facilitar o trabalho do homem.
A respeito dessas asserções, assinale a opção correta.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições falsas.
As frações são representações de partes do todo, e são escritas na forma n/d onde n e d são números naturais. E d é diferente de zero. Ao comparamos os valores de n (numerador) e d (denominador), poderemos definir o tipo da fração.
Sobre os tipos de fração existentes numere a segunda coluna de acordo com a primeira.

Está correto o que afirma em:
3, 2, 1, 4
1, 4, 3, 2
1, 2, 3, 4
3, 4, 2, 1
2, 3, 1, 4
Observe as frações abaixo,
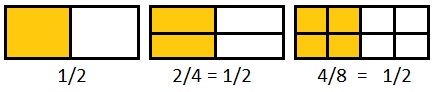
Veja que todas essas frações indicam a mesma parte da unidade considerada, ou seja, meia unidade. Dizemos que as frações 1/2, 2/4 e 4/8 são frações ___________________________, pois representam a mesma parte de um todo.
Qual das afirmativas abaixo completam corretamente a frase?
Está correto o que afirma em:
aparente
decimal
equivalente
impropria
irredutível
Leia as asserções abaixo.
I- Em uma multiplicação, o produto é sempre múltiplo de cada um dos fatores.
Porque
II- Para que um número seja múltiplo do outro, basta multiplicar esse número por um número natural.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições falsas.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A geometria é o ramo das matemáticas que se consagra ao estudo das propriedades e das medidas das figuras no espaço ou no plano. No seu desenvolvimento, a geometria usa noções tais como pontos, retas, planos e curvas, entre outras. (Disponível em: Conceito de geometria - O que é, Definição e Significado http://conceito.de/geometria#ixzz4YwcujrCW).

Euclides estudou os elementos primitivos (ponto, reta e plano) e formulou a Geometria Euclidiana. Com base nesse estudo numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
2, 3, 1, 1, 3
2, 1, 3, 1, 3
1, 3, 2, 1, 3
1, 2, 3, 1, 2
1, 2, 2, 3, 3
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Ponto, reta, reta, ponto e plano.
Ponto, plano, reta, plano e reta.
Ponto, plano, plano, ponto e reta.
Ponto, plano, reta, ponto e plano.
Plano, ponto, reta, ponto e reta.
Dois automóveis estão indo de A para B.
Observe o percurso que cada uma fez e responda a pergunta assinalando a alternativa correta.

Qual a diferença entre o percurso do carro 1 e do carro 2?

Fechamento e ou elemento neutro, distributiva, comutativa, associativa.
Fechamento e ou elemento neutro, comutativa, associativa, distributiva.
Associativa, fechamento e ou elemento neutro, distributiva, comutativa.
Fechamento e ou elemento neutro, comutativa, distributiva, associativa.
Fechamento e ou elemento neutro, associativa, comutativa, distributiva.
I - A partir do momento em que o homem abstraiu a ideia de número e a sua vida social foi se intensificando, houve a necessidade de contar conjuntos cada vez mais numerosos.
Porque:
II- Quando precisamos contar uma grande quantidade de coisas, separando os objetos em grupos, isso facilita a contagem, o que implica muitas situações. Os agrupamentos são necessários para facilitar o trabalho do homem.
A respeito dessas asserções, assinale a opção correta.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições falsas.
As frações são representações de partes do todo, e são escritas na forma n/d onde n e d são números naturais. E d é diferente de zero. Ao comparamos os valores de n (numerador) e d (denominador), poderemos definir o tipo da fração.
Sobre os tipos de fração existentes numere a segunda coluna de acordo com a primeira.

Está correto o que afirma em:
3, 2, 1, 4
1, 4, 3, 2
1, 2, 3, 4
3, 4, 2, 1
2, 3, 1, 4
Observe as frações abaixo,
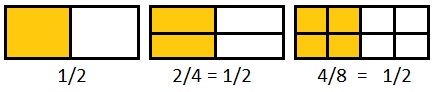
Veja que todas essas frações indicam a mesma parte da unidade considerada, ou seja, meia unidade. Dizemos que as frações 1/2, 2/4 e 4/8 são frações ___________________________, pois representam a mesma parte de um todo.
Qual das afirmativas abaixo completam corretamente a frase?
Está correto o que afirma em:
aparente
decimal
equivalente
impropria
irredutível
Leia as asserções abaixo.
I- Em uma multiplicação, o produto é sempre múltiplo de cada um dos fatores.
Porque
II- Para que um número seja múltiplo do outro, basta multiplicar esse número por um número natural.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições falsas.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A geometria é o ramo das matemáticas que se consagra ao estudo das propriedades e das medidas das figuras no espaço ou no plano. No seu desenvolvimento, a geometria usa noções tais como pontos, retas, planos e curvas, entre outras. (Disponível em: Conceito de geometria - O que é, Definição e Significado http://conceito.de/geometria#ixzz4YwcujrCW).

Euclides estudou os elementos primitivos (ponto, reta e plano) e formulou a Geometria Euclidiana. Com base nesse estudo numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
2, 3, 1, 1, 3
2, 1, 3, 1, 3
1, 3, 2, 1, 3
1, 2, 3, 1, 2
1, 2, 2, 3, 3
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Ponto, reta, reta, ponto e plano.
Ponto, plano, reta, plano e reta.
Ponto, plano, plano, ponto e reta.
Ponto, plano, reta, ponto e plano.
Plano, ponto, reta, ponto e reta.
Dois automóveis estão indo de A para B.
Observe o percurso que cada uma fez e responda a pergunta assinalando a alternativa correta.

Qual a diferença entre o percurso do carro 1 e do carro 2?
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições falsas.
As frações são representações de partes do todo, e são escritas na forma n/d onde n e d são números naturais. E d é diferente de zero. Ao comparamos os valores de n (numerador) e d (denominador), poderemos definir o tipo da fração.
Sobre os tipos de fração existentes numere a segunda coluna de acordo com a primeira.

Está correto o que afirma em:
3, 2, 1, 4
1, 4, 3, 2
1, 2, 3, 4
3, 4, 2, 1
2, 3, 1, 4
Observe as frações abaixo,
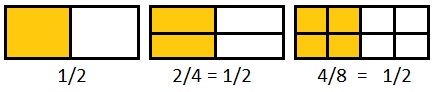
Veja que todas essas frações indicam a mesma parte da unidade considerada, ou seja, meia unidade. Dizemos que as frações 1/2, 2/4 e 4/8 são frações ___________________________, pois representam a mesma parte de um todo.
Qual das afirmativas abaixo completam corretamente a frase?
Está correto o que afirma em:
aparente
decimal
equivalente
impropria
irredutível
Leia as asserções abaixo.
I- Em uma multiplicação, o produto é sempre múltiplo de cada um dos fatores.
Porque
II- Para que um número seja múltiplo do outro, basta multiplicar esse número por um número natural.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições falsas.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A geometria é o ramo das matemáticas que se consagra ao estudo das propriedades e das medidas das figuras no espaço ou no plano. No seu desenvolvimento, a geometria usa noções tais como pontos, retas, planos e curvas, entre outras. (Disponível em: Conceito de geometria - O que é, Definição e Significado http://conceito.de/geometria#ixzz4YwcujrCW).

Euclides estudou os elementos primitivos (ponto, reta e plano) e formulou a Geometria Euclidiana. Com base nesse estudo numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
2, 3, 1, 1, 3
2, 1, 3, 1, 3
1, 3, 2, 1, 3
1, 2, 3, 1, 2
1, 2, 2, 3, 3
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Ponto, reta, reta, ponto e plano.
Ponto, plano, reta, plano e reta.
Ponto, plano, plano, ponto e reta.
Ponto, plano, reta, ponto e plano.
Plano, ponto, reta, ponto e reta.
Dois automóveis estão indo de A para B.
Observe o percurso que cada uma fez e responda a pergunta assinalando a alternativa correta.

Qual a diferença entre o percurso do carro 1 e do carro 2?

3, 2, 1, 4
1, 4, 3, 2
1, 2, 3, 4
3, 4, 2, 1
2, 3, 1, 4
Observe as frações abaixo,
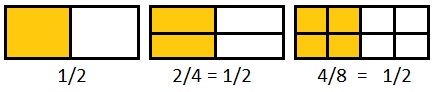
Veja que todas essas frações indicam a mesma parte da unidade considerada, ou seja, meia unidade. Dizemos que as frações 1/2, 2/4 e 4/8 são frações ___________________________, pois representam a mesma parte de um todo.
Qual das afirmativas abaixo completam corretamente a frase?
Está correto o que afirma em:
aparente
decimal
equivalente
impropria
irredutível
Leia as asserções abaixo.
I- Em uma multiplicação, o produto é sempre múltiplo de cada um dos fatores.
Porque
II- Para que um número seja múltiplo do outro, basta multiplicar esse número por um número natural.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições falsas.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A geometria é o ramo das matemáticas que se consagra ao estudo das propriedades e das medidas das figuras no espaço ou no plano. No seu desenvolvimento, a geometria usa noções tais como pontos, retas, planos e curvas, entre outras. (Disponível em: Conceito de geometria - O que é, Definição e Significado http://conceito.de/geometria#ixzz4YwcujrCW).

Euclides estudou os elementos primitivos (ponto, reta e plano) e formulou a Geometria Euclidiana. Com base nesse estudo numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
2, 3, 1, 1, 3
2, 1, 3, 1, 3
1, 3, 2, 1, 3
1, 2, 3, 1, 2
1, 2, 2, 3, 3
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Ponto, reta, reta, ponto e plano.
Ponto, plano, reta, plano e reta.
Ponto, plano, plano, ponto e reta.
Ponto, plano, reta, ponto e plano.
Plano, ponto, reta, ponto e reta.
Dois automóveis estão indo de A para B.
Observe o percurso que cada uma fez e responda a pergunta assinalando a alternativa correta.

Qual a diferença entre o percurso do carro 1 e do carro 2?
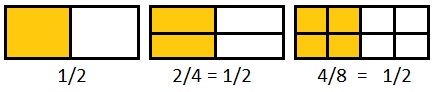
aparente
decimal
equivalente
impropria
irredutível
Leia as asserções abaixo.
I- Em uma multiplicação, o produto é sempre múltiplo de cada um dos fatores.
Porque
II- Para que um número seja múltiplo do outro, basta multiplicar esse número por um número natural.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições falsas.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A geometria é o ramo das matemáticas que se consagra ao estudo das propriedades e das medidas das figuras no espaço ou no plano. No seu desenvolvimento, a geometria usa noções tais como pontos, retas, planos e curvas, entre outras. (Disponível em: Conceito de geometria - O que é, Definição e Significado http://conceito.de/geometria#ixzz4YwcujrCW).

Euclides estudou os elementos primitivos (ponto, reta e plano) e formulou a Geometria Euclidiana. Com base nesse estudo numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
2, 3, 1, 1, 3
2, 1, 3, 1, 3
1, 3, 2, 1, 3
1, 2, 3, 1, 2
1, 2, 2, 3, 3
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Ponto, reta, reta, ponto e plano.
Ponto, plano, reta, plano e reta.
Ponto, plano, plano, ponto e reta.
Ponto, plano, reta, ponto e plano.
Plano, ponto, reta, ponto e reta.
Dois automóveis estão indo de A para B.
Observe o percurso que cada uma fez e responda a pergunta assinalando a alternativa correta.

Qual a diferença entre o percurso do carro 1 e do carro 2?
As asserções I e II são proposições falsas.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A geometria é o ramo das matemáticas que se consagra ao estudo das propriedades e das medidas das figuras no espaço ou no plano. No seu desenvolvimento, a geometria usa noções tais como pontos, retas, planos e curvas, entre outras. (Disponível em: Conceito de geometria - O que é, Definição e Significado http://conceito.de/geometria#ixzz4YwcujrCW).

Euclides estudou os elementos primitivos (ponto, reta e plano) e formulou a Geometria Euclidiana. Com base nesse estudo numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
2, 3, 1, 1, 3
2, 1, 3, 1, 3
1, 3, 2, 1, 3
1, 2, 3, 1, 2
1, 2, 2, 3, 3
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Ponto, reta, reta, ponto e plano.
Ponto, plano, reta, plano e reta.
Ponto, plano, plano, ponto e reta.
Ponto, plano, reta, ponto e plano.
Plano, ponto, reta, ponto e reta.
Dois automóveis estão indo de A para B.
Observe o percurso que cada uma fez e responda a pergunta assinalando a alternativa correta.

Qual a diferença entre o percurso do carro 1 e do carro 2?

2, 3, 1, 1, 3
2, 1, 3, 1, 3
1, 3, 2, 1, 3
1, 2, 3, 1, 2
1, 2, 2, 3, 3
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Ponto, reta, reta, ponto e plano.
Ponto, plano, reta, plano e reta.
Ponto, plano, plano, ponto e reta.
Ponto, plano, reta, ponto e plano.
Plano, ponto, reta, ponto e reta.
Dois automóveis estão indo de A para B.
Observe o percurso que cada uma fez e responda a pergunta assinalando a alternativa correta.

Qual a diferença entre o percurso do carro 1 e do carro 2?
Ponto, reta, reta, ponto e plano.
Ponto, plano, reta, plano e reta.
Ponto, plano, plano, ponto e reta.
Ponto, plano, reta, ponto e plano.
Plano, ponto, reta, ponto e reta.
Dois automóveis estão indo de A para B.
Observe o percurso que cada uma fez e responda a pergunta assinalando a alternativa correta.

Qual a diferença entre o percurso do carro 1 e do carro 2?